Breakwell Optimal Control Problem

The Breakwell optimal control problem is a simple example explaining how to handle path constraints applied to the states. It is simple enough that we will be able to derive the analytic solution of the optimal control and the optimal state trajectories. After deriving the optimal solution, we will analyze the role of the path constraint on qualities of the optimal solution.

The dynamical system in the Breakwell problem is the ubiquitous double integrator. The double integrator is a simple model of a vehicle, consisting of a position, $x(t)$, and a velocity, $v(t)$. The control input is a force applied to the vehicle.

The Breakwell problem is interesting in solving for the optimal input applied to a double integrator. The states are the position $x(t)$ and the velocity $v(t)$ so $n_x = 2$, and the single, $n_u = 1$, control input is the force $u(t)$. The time horizon of this problem is fixed, so $t \in [0,t_f]$. There is an upper bound for the position, (like a wall), so $x(t) \leq \ell$. The objective of the Breakwell problem is to move the vehicle from an initial position and velocity, $x(0) = x_0$ and $v(0) = v_0$, to a final position and velocity, $x(t_f) = x_f$ and $v(t_f) = v_f$, while minimizing the control energy.

Putting together the problem data, to solve an instance of the Breakwell problem, we must define the parameters, $$ \mathcal{P} = \{x_0,x_f,v_0,v_f,t_f,\ell\} $$

The double integrator dynamical equations are, $$ \begin{array}{l} \dot{x}(t) = v(t)\\ \dot{v}(t) = u(t) \end{array} $$ The meaning of the name double integrator becomes clear when we solve for the position in terms of the input. $$ \begin{array}{l} v(t) = \int_0^t u(\tau) d\tau + v_0\\ x(t) = \int_0^t v(\tau) d\tau + x_0 = \int_0^t \int_0^\tau u(\gamma) d\gamma + v_0 t + x_0 \end{array} $$ The path constraint, as listed in the previous section, is $x(t) \leq \ell$. This path constraint provides two requirements for the problem to be feasible, that is, $x(0) < \ell$ and $x(t_f) < \ell$. There are four events, $n_e = 4$, initial conditions and final conditions applied to both states. Finally, the cost function is the control energy, which is defined as the integral of the control input squared, $E = \int_0^{t_f} u^2(t) dt$. Note that we have not defined any units for the quantities, so that the units of this cost function may not technically be that of energy. If this is bothersome, other authors define $E$ to be the control effort but I will not bother with such semantics.

The optimal control problem is written as, $$ \begin{array}{ll} \min & J = \frac{1}{2} \int_0^{t_f} u^2(t) dt\\ \text{s.t.} && &\dot{x}(t) = v(t)\\ & \dot{v}(t) = u(t)\\ & x(t) \leq \ell\\ x(0) = x_0, \quad v(0) = v_0\\ x(t_f) = x_f, \quad v(t_f) = v_f \end{array} $$ The first line is the control energy expression, which is pre-multiplied by a factor of $\frac{1}{2}$ to avoid pesky factors of $2$, while not affecting the optimal solution.

With the problem fully defined, it is time to begin taking steps to solve it. The first step is to write the Hamiltonian. The Hamiltonian introduces the co-position state, $\lambda_x(t)$, and the co-velocity state, $\lambda_v(t)$. The Hamiltonian of the Breakwell problem is, $$ H = \frac{1}{2} u^2(t) + \lambda_x(t) v(t) + \lambda_v(t) u(t) $$ As there are path constraints, we must also write the Lagrangian of the Hamiltonian, $$ \bar{H} = H + \mu(t) x(t) $$ Additionally, as there are end-point constraints, we must also write the end-point Lagrangian, $$ \bar{E} = x(0) \nu_1 + v(0) \nu _2 + x(t_f) \nu_3 + v(t_f) \nu_4 $$ With these Lagrangians, we can write the stationarity condition which defines the optimal control. $$ \frac{\partial \bar{H}}{\partial u} = u(t) + \lambda_v(t) = 0 \quad \rightarrow \quad u(t) = -\lambda_v(t) $$ The co-position state evolves according to the dynamical equation, $$ \dot{\lambda}_x(t) = -\frac{\partial \bar{H}}{\partial x} = -\mu(t), \quad \lambda_x(0) = -\frac{\partial \bar{E}}{\partial x(0)} = -\nu_1, \quad \lambda_x(t_f) = \frac{\partial \bar{E}}{\partial x(t_f)} = \nu_3 $$ and the co-velocity state evolves according to the dynamical equation, $$ \dot{\lambda}_v(t) = -\frac{\partial \bar{E}}{\partial v} = -\lambda_x(t), \quad \lambda_v(0) = -\frac{\partial \bar{E}}{\partial v(0)} = -\nu_2, \quad \lambda_v(t_f) = \frac{\partial \bar{E}}{\partial v(t_f)} = \nu_4 $$ Finally, we must write the complementarity condition on $\mu(t)$ which determines when the path constraint is active. $$ \mu(t) \left\{ \begin{array}{lll} = 0 & \text{if} & x(t) < \ell\\ \geq 0 & \text{if} & x(t) = \ell \end{array} \right. $$

At this point, it is time to begin contemplating how to solve this problem. Two questions one should ask themselves to determine the practicality of solving an optimal control problem analytically are the following:

If all of the dynamical equations are linear, then it is likely the optimal control problem can be solved in terms of matrix functions. In many practical situations this often good enough as there are fast and accurate numerical methods for solving matrix equations. An example of this is the famous LQR optimal control problem.

If even some of the dynamical equations are nonlinear, then the chance that the optimal control problem is solvable analytically drops precipitously. There are very few systems of nonlinear dynamical equations which can be solved.

By sequential dynamics, I am referring to the dynamical systems' graph representation. The graph representation of a dynamical system defines a node for each time-varying state, and directed edges are added from node $x_i$ to $x_j$ if $x_i$ appears in the equation for $\dot{x}_j$. If the resulting graph has no loops, then the dynamics are sequential, which means that we may solve for each dynamical equation separately. If there is a loop, then all of the dynamical equations for the states in that loop must be solved simultaneously, which typically increases the difficulty.

To gain some insight into this problem, a first draft of the numerical solver is written in order to start gathering some data about the optimal solution. I use the numerical solver $\mathcal{PSOPT}$ as it is (i) free, (ii) open-source, (iii) straight-forward to use. More details about using $\mathcal{PSOPT}$ can be found in the section [PSOPT USAGE SECTION].

The first step to write the code is to define a structure that contains all of the parameters that define a particular instance of the Breakwell problem.

          typedef struct {
            double x0;   // The inital position
            double v0;   // The initial velocity
            double xf;   // The final position
            double vf;   // The final velocity
            double ell;  // The upper bound applied to the position
            double tf;   // The final time
          } params_t;
          

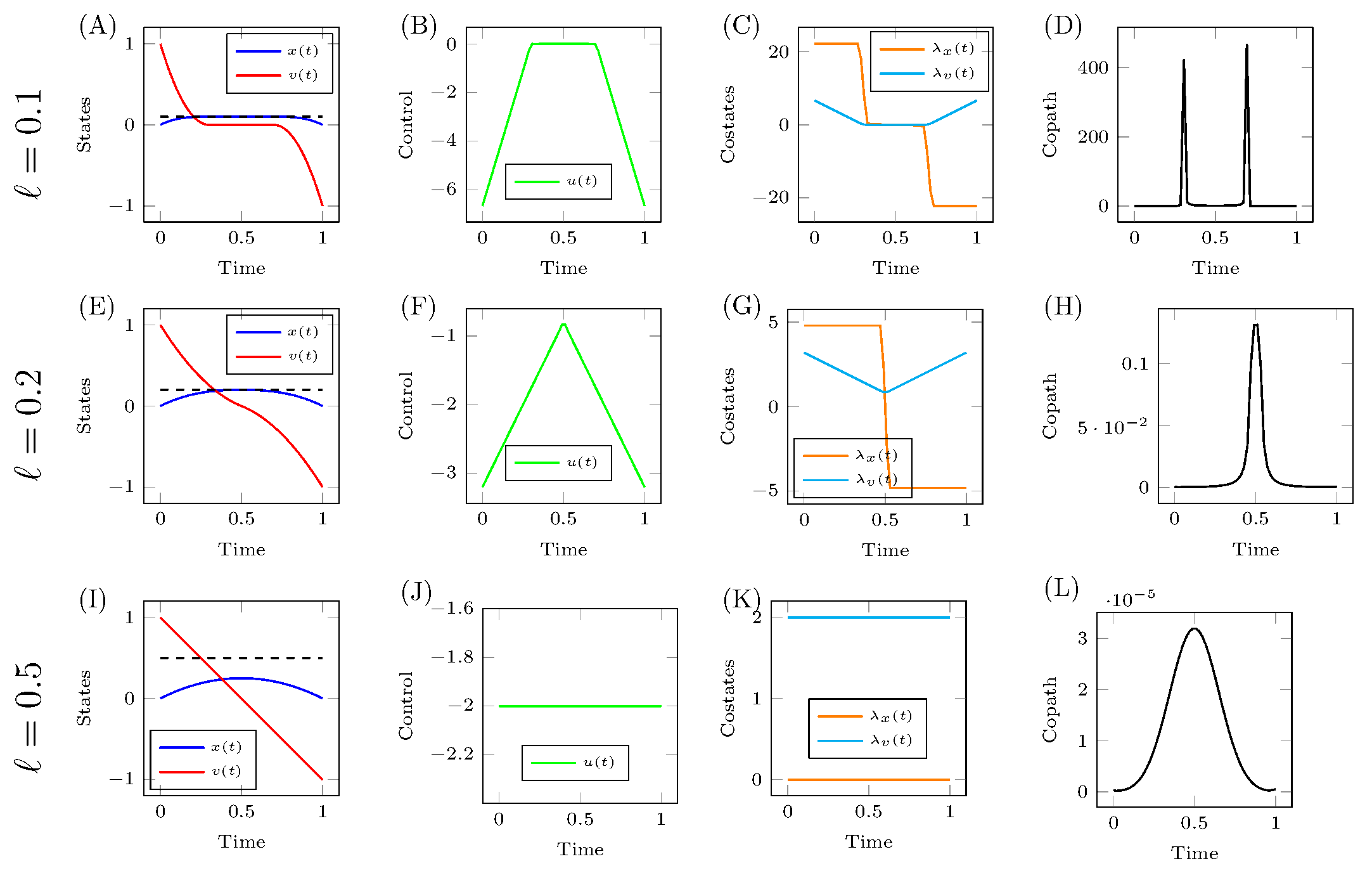
Some numerical results for select choices of $\ell$ are shown in the figure to right. The data is chosen as, $$ x_0 = 0, \quad v_0 = 1, \quad x_f = 0, \quad v_f = -1, \quad t_f = 1 $$ and $\ell$ is set as $0.1$, $0.2$, and $0.5$. There appear to be two distinct regimes, when the optimal position trajectory is equal to $\ell$ for some interval of time and when it does not, with a value of $\ell$ for which $x(t) = \ell$ for only a single instance in time. If $\ell$ is large enough that $x(t)$ remains strictly smaller than it, then we can neglect the path constraint and solve the optimal control problem as it does not affect the solution. On the other hand, if there exists a time interval for which $x(t) = \ell$, then we must investigate the behavior of $\mu(t)$. In the following, the case when $x(t) = \ell$ for some interval of time is investigated in detail. The other case, when $x(t) < \ell$ for the whole duration of the optimal control, will be briefly discussed at the end.

Let us define the three intervals of time as $\mathcal{I}_1$, $\mathcal{I}_2$ and $\mathcal{I}_3$.

1. For $t \in \mathcal{I}_1 = [0,t_1)$, the position $x(t) < \ell$ so that $\mu(t) = 0$.
2. For $t \in \mathcal{I}_2 = (t_1,t_2)$, the position is now at $x(t) = \ell$ so that $\mu(t) \geq 0$.
3. For $t \in \mathcal{I}_3 = (t_2,t_f]$, the position is once again $x(t) < \ell$ and so $\mu(t) = 0$.

In the second interval, we see that the position is stationary, $x(t) = \ell$. This implies that the velocity must be zero, $v(t) = 0$, which further implies that $\dot{v}(t) = 0$ as well. By the same argument this in turn implies that $u(t) = 0$, $\lambda_v(t) = 0$, $\lambda_x(t) = 0$, and thus $\mu(t) = 0$ over the second interval, $t \in \mathcal{I}_2$.

It appears now that $\mu(t) = 0$ over all three intervals! This is not the case though, since we have not defined the behavior of any of the quantities at the boundary times, $t_1$ and $t_2$. At these points, the co-path $\mu(t)$ may have discontinuities. Note that this appears to be the case according to the numerical results when $\ell = 0.1$.

This brings into stark clarity the deficiencies of numerical optimal control solvers. If the optimal solution consists of point discontinuities, such as Dirac delta functions, then the numerical solver will never be able to find the true optimal solution! A discussion on how to use this kind of information to better formulate optimal control problems for numerical solvers is given in at the end of this page.

With the above discussion on the solvability of the differential equations and the preliminary numerical results, let us solve for the optimal solution. The first step is to characterize the co-path $\mu(t)$, $$ \mu(t) = A_1 \delta(t,t_1) + A_2 \delta(t,t_2) $$ where $A_1,A_2 \geq 0$ and $0 \leq t_1 \leq t_2 \leq t_f$. The Dirac delta function $\delta(t,t_1)$ is defined as satisfying the equation for any $\epsilon > 0$, $$ \int_{t_1-\epsilon}^{t_1+\epsilon} \delta(t,t_1) dt = 1 $$ We can now solve for the co-position state, $\lambda_x(t)$. $$ \lambda_x(t) = \left\{ \begin{array}{lll} -\nu_1 & \text{if} & t \in \mathcal{I}_1\\ 0 & \text{if} & t \in \mathcal{I}_2\\ \nu_3 & \text{if} & t \in \mathcal{I}_3 \end{array} \right. $$

With the co-position known to be a step function, we can now integrate to find the reverse co-velocity. $$ \lambda_v(t) = \left\{ \begin{array}{lll} \nu_1(t-t_1) & \text{if} & t \in \mathcal{I}_1\\ 0 & \text{if} & t \in \mathcal{I}_2\\ \nu_3(t-t_2) & \text{if} & t\in\mathcal{I}_3 \end{array} \right. $$

We also get a relationship between the co-event parameters for $\lambda_v(0) = -\nu_1 t_1 = -\nu_2$. From the stationarity condition, we had previously found that, $$ u(t) = -\lambda_v(t) = \left\{ \begin{array}{lll} \nu_1 (t_1-t) & \text{if} & t \in \mathcal{I}_1\\ 0 & \text{if} & t \in \mathcal{I}_2\\ \nu_3 (t-t_2) & \text{if} & t \in \mathcal{I}_3 \end{array} \right. $$ With the optimal control known, we can now integrate it to find the optimal time-trajectory of the velocity. $$ v(t) = \left\{ \begin{array}{lll} \frac{v_0 (t-t_1)^2}{t_1^2} & \text{if} & t \in \mathcal{I}_1\\ 0 & \text{if} & t \in \mathcal{I}_2\\ \frac{v_f(t-t_2)^2}{(t_f-t_2)^2} & \text{if} & t \in \mathcal{I}_3 \end{array} \right. $$

With the optimal velocity known, the only quantity that remains is the optimal time-trajectory of the position, found by integrating the velocity. $$ x(t) = \left\{ \begin{array}{lll} \frac{v_0}{3t_1^2} \left( t^3 - 3 t_1 t^2 + 3t_1^2 t \right) + x_0 & \text{if} & t \in \mathcal{I}_1\\ \ell & \text{if} & t \in \mathcal{I}_2\\ \ell + \frac{v_f}{3} \frac{(t-t_2)^3}{(t_f-t_2)^2} & \text{if} & t \in \mathcal{I}_3 \end{array} \right. $$

In the details of the derivation of $x(t)$ section above, we found the relation for the first switching time, $$ \frac{v_0}{3} t_1 + x_0 = \ell \quad \rightarrow \quad t_1 = \frac{3(\ell-x_0)}{v_0} $$ Applying the final position condition gives the relation for the second switching time, $$ x_f = \ell + \frac{v_f}{3} (t_f-t_2) \quad \rightarrow \quad t_2 = \frac{3(\ell-x_f)}{v_f} + t_f $$ With these expressions, we can determine when the three interval solution is the optimal solution using the series of inequalities, $$ 0 \leq t_1 \leq t_2 \leq t_f $$

1. The first interval states that $$ 0 \leq \frac{3(\ell-x_0)}{v_0} $$ which implies that $v_0 > 0$ since $x_0 < \ell$
2. The third interval states that $$ \frac{3(\ell-x_f)}{v_f} + t_f \leq t_f $$ which implies that $v_f < 0$ since $x_f < \ell$
3. The second interval states that $$ \frac{3(\ell-x_0)}{v_0} \leq \frac{3(\ell-x_f)}{v_f} + t_f $$ Solving this inequality for $\ell$ yields, $$ \ell \leq \ell_{\max} = \frac{3x_0v_f - 3x_fv_0 + v_fv_0t_f}{3(v_f-v_0)} $$ If $\ell > \ell_{\max}$ then $x(t) \neq \ell$ for any time and the optimal solution consists of a single continuous segment, like in the numerical results above when $\ell = 0.5$.

For completeness, the solution for the case $x(t) \neq \ell$ is solved as well. In this case, $\mu(t) = 0$ for all time and so the co-position is a constant, $$ \lambda_x(t) = \int_t^{t_f} \mu(\tau) d\tau + \nu_3 = \nu_3 $$ From the initial co-position condition, we have $\nu_3 = -\nu_1$. The co-velocity is then a linear function, $$ \lambda_v(t) = \int_t^{t_f} \lambda_x(\tau) d\tau + \nu_4 = \nu_3(t_f-t) + \nu_4 $$ From the initial co-velocity condition we have that $\lambda_v(0) = \nu_3 t_f + \nu_4 = -\nu_2$. The optimal control must also be linear, $$ u(t) = \nu_3 (t-t_f) - \nu_4 $$ The optimal velocity is then quadratic, $$ v(t) = \int_0^t u(\tau) d\tau + v_0 = \left( \frac{t^2}{2} - t_ft \right) \nu_3 - \nu_4 t + v_0 $$ The optimal position must then be cubic, $$ x(t) = \left( \frac{t^3}{5} - t_f \frac{t^2}{2} \right) \nu_3 - \frac{t^2}{2} \nu_4 + v_0 t + x_0 $$ We can find the co-final conditions, $\nu_3$ and $\nu_4$, from the final conditions for the position and velocity. $$ \begin{array}{ll} v_f & = -\frac{t_f^2}{2} \nu_3 - t_f \nu_4 + v_0\\ x_f & = -\frac{t_f^3}{3} \nu_3 - \frac{t_f^2}{2} \nu_4 + v_0 t_f + x_0 \end{array} $$ Rearranging this linear system into the usual form, $$ \left[ \begin{array}{cc} -\frac{t_f^2}{2} & -t_f \\ -\frac{t_f^3}{3} & -\frac{t_f^2}{2} \end{array} \right] \left[ \begin{array}{c} \nu_3 \\ \nu_4 \end{array} \right] = \left[ \begin{array}{c} v_f - v_0 \\ x_f-x_0-v_0t_f \end{array} \right] $$ The solution to this system of equations is, $$ \begin{array}{rcl} \nu_3 & = & \frac{6}{t_f^3} \left[ 2(x_0-x_f) + t_f(v_0+v_f) \right]\\ \nu_4 & = & \frac{2}{t_f^2} \left[ 3(x_f-x_0) - t_f (v_0 + 2v_f) \right] \end{array} $$ With these results, the optimal control input in this case is, $$ u(t) = \frac{2}{t_f^3} \left[ (6(x_0-x_f) +3 t_f(v_0+v_f)) t + 3t_f(x_f-x_0) - t_f^2(2x_0 + v_f) \right] $$ The cost can then be found by integrating $u^2(t)$, $$ J = \frac{1}{2} \int_0^{t_f} u^2(t) dt = \frac{2}{t_f^3} \left[ 3(x_f-x_0)^2 + t_f^2 (v_f+v_0)^2 - t_f^2 v_0v_f + 3t_f (v_0x_0 - v_0x_f + v_f x_0 - v_f x_f) \right] $$ Note that the cost now depends on the final $t_f$.

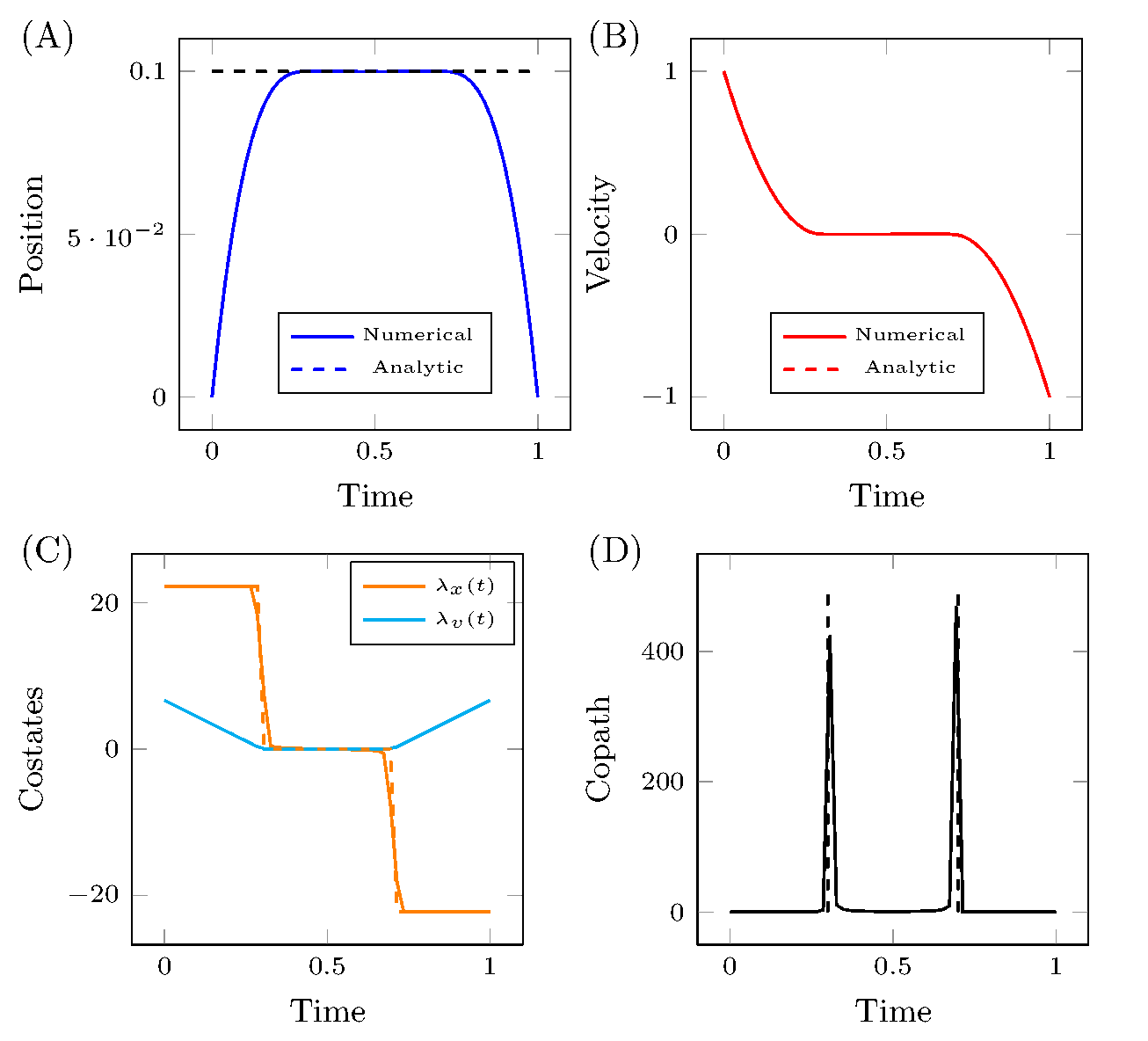A comparison of the three interval solution to the numerical results for $x_0 = 0$, $v_0 = 1$, $x_f = 0$, $v_f = -1$, $t_f = 1$, and $\ell = 0.1$ is shown on the left. The numerical and analytical results for the position and the velocity are indistinguishable. The difference becomes apparent for $\lambda_x(t)$ which is a step function and the copath $\mu(t)$ which consists of two delta functions. It is these types of discontinuities, present in many optimal control problems with constraints becoming active and inactive at different points in time, that make solving optimal control problems numerically difficult. Nonetheless, as most optimal control problems are analytically intractable, we must accept these difficulties. The engineer must use the analytic tools we have available to properly interpret the numerical results, detecting discontinuities

Hello, my name is Isaac Klickstein, currently living in Albuquerque, New Mexico. I am working on my PhD in the mechanical engineering department at the University of New Mexico. My research involves optimal control, network science, and regular graphs. I will be graduating in December, 2019 and moving to New England in January, 2020.

• iklick@unm.edu
• Department of Mechanical Engineering MSC01 1150
  1 University of New Mexico
  Albuquerque, NM 87131