Target Control (and Balance Control) [INCOMPLETE]

Let $\mathcal{G} = (\mathcal{V},\mathcal{E})$ be a graph with $|\mathcal{V}| = n$ nodes and edges $\mathcal{E} \subset \mathcal{V} \times \mathcal{V}$. Each edge $(v_i,v_j) \in \mathcal{E}$ is read as the edge from $v_i$ to $v_j$. The neighbors of node $v_i \in \mathcal{V}$ is defined as the set $\mathcal{N}_i \subseteq \mathcal{V}$ where $v_j \in \mathcal{N}_i$ if $(v_j,v_i) \in \mathcal{E}$. We assume that there are self-loops at every node, i.e., $(v_i,v_i) \in \mathcal{E}$ for all $v_i \in \mathcal{V}$. Let $A \in \mathbb{R}^{n \times n}$ be the adjacency matrix where $A_{ij} \in \mathbb{R}$ for every $(v_j,v_i) \in \mathcal{E}$ and $A_{ij} = 0$ if $(v_j,v_i) \notin \mathcal{E}$. We call $A_{ij}$ the edge weight associated with edge $(v_j,v_i)$.

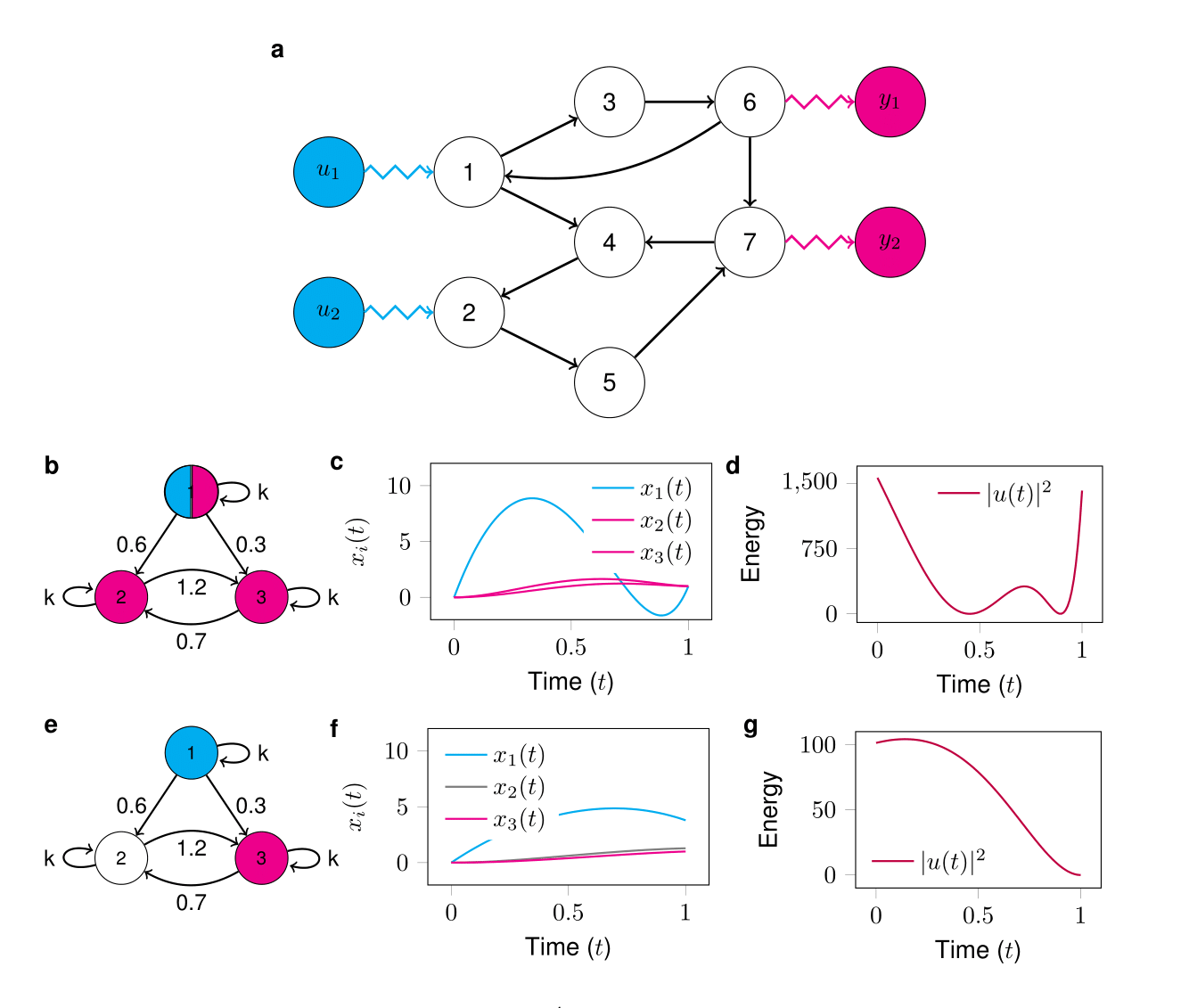We define two subsets of $\mathcal{V}$ called the driver nodes, $\mathcal{D} \subseteq \mathcal{V}$, and the target nodes, $\mathcal{T} \subseteq \mathcal{V}$. Each node has an associated time-varying signal called $x_i(t)$ which evolves according to the following linear dynamical equation: $$ \dot{x}_i(t) = \sum_{v_j \in \mathcal{N}_i} A_{ij} x_j(t) + \sum_{v_k \in \mathcal{D}} \delta_{i,k} u_k(t) $$ Each node $v_k \in \mathcal{D}$, $k = 1,\ldots,m$ is assumed to have an external, time-varying, input attached which we are free to design. We would like to drive each node $v_{\ell} \in \mathcal{T}$, $\ell = 1,\ldots,p$, to some particular value.