Research
Our research broadly focuses on advancing quantum computing and simulation technologies while developing new tools at the intersection of quantum information science, nuclear physics, and high-energy physics. We work with state-of-the-art quantum hardware to push the frontiers of technology through algorithm design, quantum simulation, and device benchmarking. Our primary focus lies in non-equilibrium phenomena, random-measurement protocols, and entanglement tomography, with applications spanning high-energy and nuclear physics, as well as connections to atomic, molecular, and optical (AMO) physics and condensed matter physics.

Quantum Computation and Simulation for Nuclear and High-Energy Physics
We co-design quantum simulation and tomography techniques that integrate hardware, algorithms, and physics objectives to address grand challenges in high-energy and nuclear physics. A central focus is the development of methods to measure unconventional observables, particularly quantum information resources such as entanglement, coherence, and non-stabilizerness.
Nonequilibrium Phenomena
Nonequilibrium phenomena, such as thermalization, scattering, or dynamical phase transitions, present fundamental challenges that are well-suited for quantum computation. Understanding thermalization in high-energy and nuclear physics remains an open problem from both analytical and computational perspectives. Our research investigates the role of entanglement in nonequilibrium many-body dynamics and lattice gauge theories.
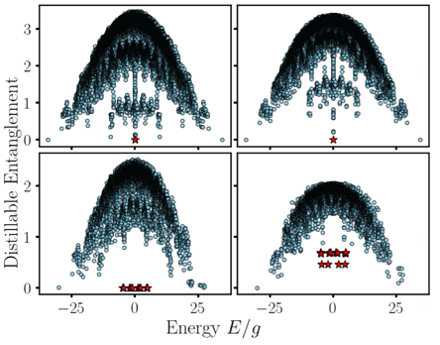
Entanglement and Complexity
Computational complexity characterizes what makes a problem difficult to solve, while in fundamental physics, complexity distinguishes quantum from classical behavior. We develop analytical and numerical tools to quantify quantum complexity, with a particular focus on entanglement and non-stabilizerness, and explore applications to heavy-ion collisions and early-universe physics.
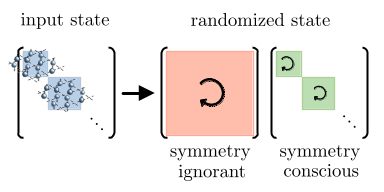
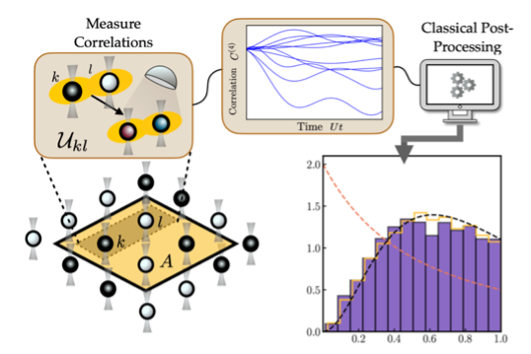
Random Measurement Tomography
Quantum states encode exponentially large amounts of information, yet measurements typically reveal only a small fraction of it. Randomized measurement protocols provide a powerful approach to overcoming this limitation, enabling access to key physical quantities with relatively few measurements. We apply these techniques to study entanglement in quantum many-body systems and explore broader implications for quantum simulation and information processing.

Benchmarking and Verification
What are meaningful applications for quantum computers, i.e., where they prove more powerful than classical computing? The answer is subtle: classical algorithms, in particular for science problems, have been developed over decades and are powerful, and claims of quantum advantage depend strongly on which observables are computed and with what precision. We develop quantitative metrics and verification strategies to benchmark quantum simulations for early fault-tolerant devices, including classical stress tests that identify regimes where genuine quantum advantage may emerge.