Open Resources

On-going Projects

1. Fourth-order RANS-based turbulence closure

High-order statistical closures based on the Reynolds-averaged Navier-Stokes (RANS) equations have been proposed for turbulence modeling in the 40s, but have not received proper attention even though this is the only approach, where the amount of physics contained in the equations solved is explicitly linked to the number of these equations. Indeed, a solution of the complete set of RANS equations is infinitely close to the accurate solution of the Navier-Stokes equations. Thus, by increasing the closure order, the epistemic uncertainty in a turbulence model, which is due to the lack of the flow physics knowledge, is reduced and the accuracy of model predictions can be improved.

This project advances the development of a fourth-order statistical closure (FORANS closure) capable of accurate description of wall-bounded turbulent flows in a wide range of flow parameters without artificial wall functions and other corrections of the transport equations and without varying values of model coefficients. Reduced-order closures can be developed from the FORASN closure for industrial applications on physics-based grounds.

As in other RANS models, the modeling of terms associated with turbulent diffusion, interaction of turbulent velocity and pressure fields, and dissipation are required to close the FORANS equations. What makes a FORANS closure more attractive than all other RANS models is a possibility to model the turbulent diffusion terms using truncated Gram-Charlier series expansions (GCSE). These models are simple algebraic expressions obtained rigorously with no unknown coefficient involved. They include only velocity moments of the orders lower than the 4th and are applicable in non-Gaussian turbulent flows.

Validation of the truncated GCSE in various flow gemetries and flow parameters is one of the project goals.

S. V. Poroseva, B. E. Kaiser, J. A. Sillero, S. M. Murman, “Validation of a Closing Procedure for Fourth-Order RANS Turbulence Models with DNS Data in an Incompressible Zero-Pressure-Gradient Turbulent Boundary Layer,” Int. J. Heat Fluid Flow, 2015.

Developement of models for velocity/pressure-gradient (VPG) correlations in the FORANS equations is the other goal. We have demonstrated that data-driven models for such correlations are the most accurate option in wall-bounded flows. These models are linear functions of molecular and turbulent diffusions as well as of the productions terms. The model coefficients remain constant in various considered flow geometries in a wide range of Reynolds numbers, and in a presence of a flow separation. No wall corrections are required.

S. V. Poroseva, S. M. Murman, “ Sensitivity of a New Velocity/Pressure-Gradient Model to Reynolds Number,” Proc. TSHP-10, Chicago, IL, July 6-July 9, 2017.
AIAA2015-3067
S. V. Poroseva, S. M. Murman, “ Reynolds-Stress Simulations of Wall-Bounded Flows Using a New Velocity/Pressure-Gradient Model,” Proc. TSHP-9, Melbourne, Australia, June 30-July 3, 2015.
S. V. Poroseva, S. M. Murman, “ On Modelling Velocity/Pressure-Gradient Correlations in Higher-Order RANS Statistical Closures,” Proc. the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, December 8-11, 2014.
AIAA2014-2207

2. DNS of a spatially developing incompressible mixing layer

Flow conditions used in DNS are close to those from the experiments by Bell & Mehta (1990), where untripped boundary layers co-flowing on both sides of a splitter plate mix downstream the plate. No artificial perturbations are used in simulations to trigger the flow transition to turbulence. DNS are conducted using the spectral-element code Nek5000.

We have investigated sensitivity of the DNS results to the computational parameters such as the splitter plate thickness, dimensions of the computational domain in the spanwise, transverse, and streamwise directions, time step, and the boundary layer characteristics at the trailing edge of the splitter plate. The choice of parameters was driven by a search for their optimal combination for conducting cost-effective accurate DNS in a domain long enough to achieve a self-similar regime in a turbulent mixing layer.
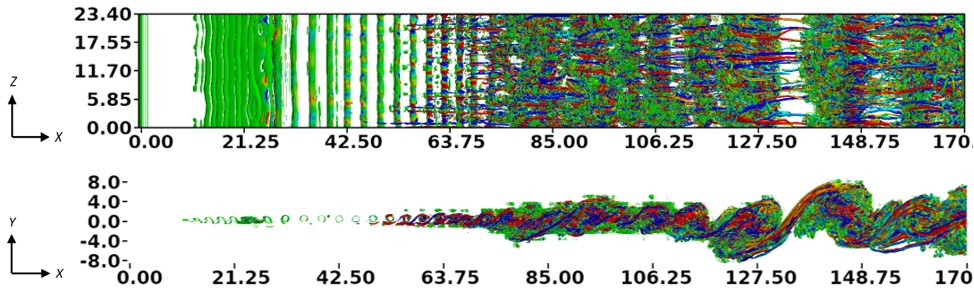
AIAA2017-3641
AIAA2018-3226.

Resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center. Flow visualization using FieldView software was possible thanks to Intelligent Light who provided an academic license.

3. RANS-DNS simulations for uncertainty quantification in DNS data

In RANS-DNS simulations, the exact RANS equations are solved, with no modeling involved. All budget terms except for the molecular diffusion are substituted with the data collected from DNS for these terms. In such a formulation, all equations are uncoupled, that is, there is no interdependency of their solutions. We demonstrated that the dominant source of uncertainty in the results of such simualtions is inaccuracies in the DNS budgets used in the simulations, which makes the RANS-DNS simulations a plausible framework for quantifying the total uncertainty in statistical data collected from DNS. We also proposed metrics for a quantitative analysis of the DNS budget accuracy. Rigor of the proposed uncertainty quantification procedure, availability of reliable RANS solvers, and low computational cost of such simulations makes the proposed approach for evaluating the DNS data accuracy accessible and attractive to a broad community. Currently, RANS-DNS simulations were conducted in incompressible planar wall-bounded turbulent flows.

S. V. Poroseva, J. D. Colmenares F., S. M. Murman, “"On the accuracy of RANS simulations with DNS data," Physics of Fluids , 2016, 28(11). DOI: 10.1063/1.4966639 manuscript.

We also investigated the effect of the DNS data averaging time on the accuracy of RANS-DNS simulations in a fully-developed turbulent channel flow. It was found that statistical errors in DNS data were reduced at earlier averaging times, revealing a presence of the systematic error in the DNS data, which has a significant effect on the RANS-DNS simulation results and cannot be reduced with increasing the averaging time. Its origin remains unknown and is a subject of our current investigation. AIAA2016-3940

Open Resources

OpenFOAM source files

for two benchmark cases: a 2D ZPG boundary layer over a flat plate and a 2D bump-in-channel flow (see description at TMBWG), with the standard formulations of Spalart-Allmaras, Wilcox’s 2006 version of k-ω, and SST 1994 turbulence models (also as described at the TMBWG website) can be downloaded here as a single zip file. Changes to the original OpenFOAM files are documented here . Important note: the source files are for the OpenFOAM version 2.3.0 only. Any later version of OpenFOAM will, unfortunately, require additional "cleaning" to get simulation results comparable to those of the NASA codes. If you use our files, please refer to our paper AIAA2014-2087, where the results obtained with these files were initially presented. This will be highly appreciated.

DNS data for 3rd, 4th, and 5th-order velocity moments in a zero-pressure gradient boundary layer over a flat plate at Re_θ = 4100 and 5200.

The data are described in S.V. Poroseva, B.E. Kaiser, J.A. Sillero, S.M. Murman, “Validation of a Closing Procedure for Fourth-Order RANS Turbulence Models with DNS Data in an Incompressible Zero-Pressure-Gradient Turbulent Boundary Layer,” Int. J. Heat and Fluid Flow, 2015, http://dx.doi.org/10.1016/j.ijheatfluidflow.2015.06.010. They can be downloaded here as a single zip-file. The zip-file contains 6 data files that can be open with any text editor.

Experimental data for stationary and rotating cylindrical pipe flow

The data were first published in Zaets, P. G., Kurbatskii, A. F., Onufriev, A. T., Poroseva S. V., Safarov, N. A., Safarov, R. A., Yakovenko S. N. “Experimental study and mathematical simulation of the characteristics of a turbulent flow in a straight circular pipe rotating about its longitudinal axis.” J. Appl. Mech. and Tech. Physics, 1998, 39(2), pp. 249-260. (See also A. F. Kurbatskii and S. V. Poroseva, “Modelling turbulent diffusion in a rotating cylindrical pipe flow.” Int. J. Heat and Fluid Flow, 1999, 20(3), pp. 341-348. ) The data can be downloaded here as a single xlsx-file.